排序算法总结

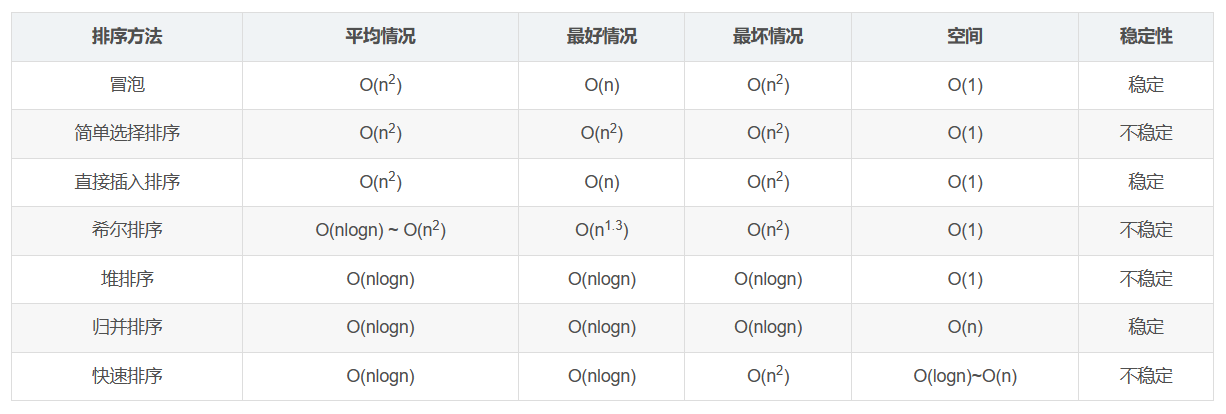
排序算法总结
三水番总结
- 为了绝对的速度选快排
- 为了省空间选堆排
- 为了稳定性选归并
插入排序O(N^2),但是常数项小;快速排序O(NlogN),但是常数项高。也就是N很大的时候,采用快排;当N比较小的时候,采用插排。
Java中Arrays.sort()方法,如果传入的是基础类型,系统是采用快排进行排序的(因为此时的稳定性是无意义的,而快排比堆排更快);如果传入的是非基础类型,系统是采用归并排序进行排序的(因为此时可能是需要稳定性的)。不管是快速排序还是归并排序,在二分的时候小于_**32**_的数据量依旧会使用二分插入排序。
1、冒泡排序:相邻交换
- 时间复杂度:O(N^2)
- 空间复杂度:O(1)
- 稳定性:稳定
冒泡排序是一种交换排序,核心是冒泡,把数组中最小的那个往上冒,冒的过程就是和他相邻的元素交换。
冒泡排序有一种优化算法,就是立一个 flag,当在一趟序列遍历中元素没有发生交换,则证明该序列已经有序。
- 冒泡排序始终在调整‘逆序’,交换次数为排列中逆序的个数
2、简单选择排序:找到最大或最小交换
- 时间复杂度:O(N^2)–>元素
比较次数始终为n(n-1)/2;元素移动次数不超过3(n-1),最好为0(有序) - 空间复杂度:O(1)
- 稳定性:不稳定
首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。
3、插入排序:找到最大或最小插入
- 时间复杂度:O(N^2)
- 空间复杂度:O(1)
- 稳定性:稳定
插入排序的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
当数据基本有序时,采用插入排序可以明显减少数据交换和数据移动次数,进而提升排序效率。 可以将插入排序作为快速排序的补充,用于少量元素的排序。
4、快速排序(递归)
- 时间复杂度:O(NlogN)
- 空间复杂度:O(logN)
- 稳定性:不稳定
快速排序使用分治法(Divide and conquer)策略来把一个串行(list)分为两个子串行(sub-lists)。
通过一趟排序将待排记录分隔成独立的两部分,其中一部分记录的关键字均比另一部分的关键字小,则可分别对这两部分记录继续进行排序,以达到整个序列有序。
- 枢轴元素在一趟排序后处于最终位置
- 最好情况:每次划分将待排序列划分为等长两部分
5、归并排序(递归)
- 时间复杂度:O(NlogN)
- 空间复杂度:O(N)
- 稳定性:稳定
空间复杂度O(N)使得在数据量特别大的时候(例如,1千万数据)几乎不可接受。
6、堆排序(前n大的数首选)
- 时间复杂度:O(NlogN)
- 建堆:o(N)
- 调整堆:o(logN) or o(h)
- 空间复杂度:O(1)
- 稳定性:不稳定
建堆:
- 构建大顶堆:从最后一个非叶子节点(n/2-1)开始,自底向上调整堆,直到根节点。注意每次交换后,都要对下一层的子堆进行递归调整,因为交换后有可能破坏已调整子堆的结构。
eg: 本文链接:https://blog.csdn.net/zhizhengguan/article/details/106826270
2. 假设给定无序序列结构:
3. 从最后一个非叶子结点开始(叶结点自然不用调整,第一个非叶子结点 arr.length/2-1=5/2-1=1,也就是下面的6结点),从左至右,从下至上进行调整。【9下沉之后,9变成了叶子节点,因此不会对子叶产生影响】
堆排序就是把大顶堆堆顶的最大数取出,将剩余的堆继续调整为最大堆,再次将堆顶的最大数取出,这个过程持续到剩余数只有一个时结束。
4. 找到第二个非叶节点4 【3/2 - 1 = 0】,由于[4,9,8]中9元素最大,4和9交换。【4下沉之后,变动了的子树必须重新调整】
此时,我们就将一个无需序列构造成了一个大顶堆。
** 解决“前N大的数”一类问题时,几乎是首选算法。**
- 最后一个节点是第$\lfloor n/2 \rfloor$个节点的孩子
- 从根节点到任意叶节点的路径都是有序的